Pierre Gaulon

Pierre Gaulon Github pages

View on GitHub

Introduction

I had the occasion to be exposed to Chinese cryptography standards published by the Chinese Commercial Cryptography Administration Office: SM2, SM3, and SM4. SM stands for ShangMi.

This article aims to guide any further usage of such cryptography standards. It is a bit long to cover everything: jump directly to the part you are interested in.

Elliptic Curve Cryptography (ECC)

ECC is one of the approaches to public-key cryptography.

Public-key cryptography

Public-key cryptography relies on the generation of 2 keys:

From a public key, it is not possible (i.e. it takes more than centuries to compute) to know its private key. It is possible to prove the possession of a private key without disclosing it. This proof can be verified by using its corresponding public key. This proof is called a digital signature.

High level functions

ECC can perform signature and verification of messages (authenticity). ECC can also perform encryption and decryption (confidentiality), however, not directly. For encryption/decryption it needs the help of a shared secret, namely a key.

ECC delivers the same protection as RSA (Rivest-Shamir-Adleman) with a smaller key size. Smaller keys means less operations and less storage. For instance an ECC 256bits key should provide the same level of security as an RSA key of 3072bits.

Theory summary

Following the very well explained guides from Hans Knutson on Hacker Noon and CryptoBook from Svetlin Nakov, this section aims to provide a sense of different parameters which will be found in SM2 libraries, and what they correspond to.

Key generation

As a comparison, RSA is based on prime number factorization and its private key is composed of 2 long prime numbers (called p and q). The modulus m is the product pq=m which constitutes the public key. The size of m in bits is the key size of RSA. From the knowledge of m, it is hard to decompose it back into the 2 prime numbers p and q.

ECC is based on the discrete logarithm of elliptic curve elements. An elliptic curve consists of all the points of coordinates (x,y) verifying y² = x³+ax+b. For instance Bitcoin uses the curve called secp256k1 which verifies y² = x³+7. It is possible to add 2 points of that curve together:

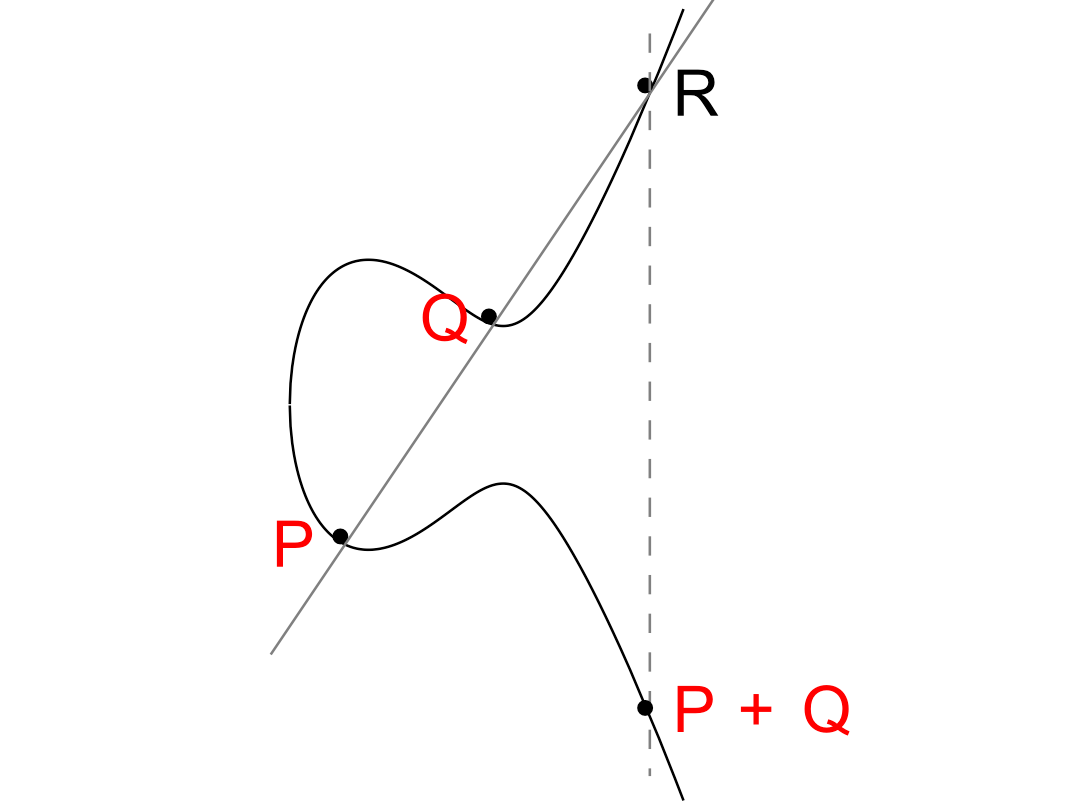EC addition
From https://iis-projects.ee.ethz.ch/images/d/de/Elliptic_curve_addition.png

Or to add a point to itself:

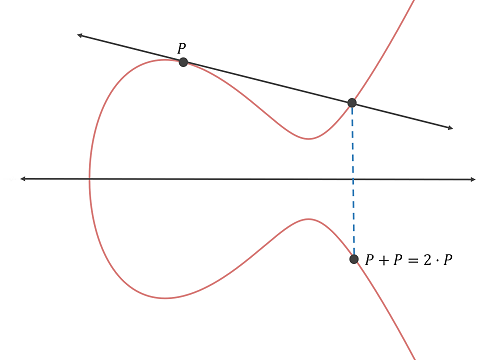EC addition
From http://www.herongyang.com/EC-Cryptography/Elliptic-Curve-with-Same-Point-Addition.png

Moreover to make sure that points stay within reasonable coordinates, the curve y² = x³+ax+b is wrapped around itself using a modulus p: y² mod p = (x³ + ax + b) mod p

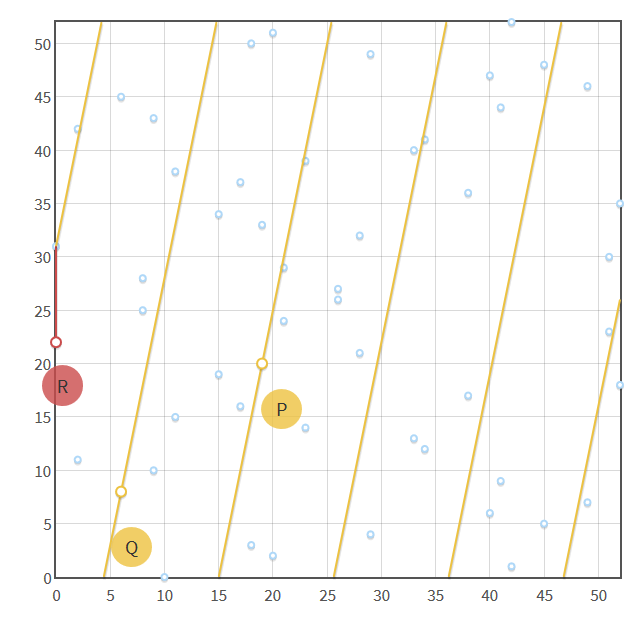Curve modulo
From https://hackernoon.com/what-is-the-math-behind-elliptic-curve-cryptography-f61b25253da3

The ECC private key is given by choosing a base point P (also called Generator point G) on the wrapped curve, and adding itself x times (which defines the operation • as x•P = P + ... + P, x times), with x a random 256bits integer. The resulting point from x•P will be called X, and is fast to compute thanks to exponentiation by squaring. The coordinates of the base point P are known for a type of curve and the coordinates of X are the public key. The private key is x which by definition has a size of 256bits. From the end point X it is hard to find the number of iterations x.

Digital Signature

The signature algorithm for ECC is called Elliptic Curve Digital Signature Algorithm, or ECDSA. Without going into the details, signing a message m is done by first hashing it. A random integer k is chosen and used to multiply the base point P. The result of that signature consists in 2 elements: r and s.

An important note is that since there is a random number k in the signature, 2 signatures of the same message m will not look the same. This process is called the Schnorr Identification Protocol.

Back to SM2/SM3/SM4

One of the main open source implementation of SM2/SM3/SM4 algorithms is GmSSL (Gm stands for Guomi). Other implementations exist, such as gmsm in Golang, gmssl in Python, or Chinese Financial Certification Authority (CFCA) SADK in Java.

My goal was to port Java code to Golang: reverse engineering the usage of CFCA SADK in this use case, and adapt gmsm to it. The hashing algorithm SM3 and the encryption algorithm SM4 were used as-is and could be ported from one language to another using the equivalent functions.

From a classic REST API POST, with several parameters, few additional security operations are taking place:

The second step was the most interesting as the Golang library was not implementing the PKCS7 formatting of the signature: only American standards were supported.

How to get keys

For testing purposes, the private key used for SM2 signing was provided to us, along with a passphrase. Of course, in production systems the private key is generated and kept private. The file extension is .sm2, the first step was to make use of it.

It can be parsed with:

$ openssl asn1parse -in file.sm2

    0:d=0  hl=4 l= 802 cons: SEQUENCE
    4:d=1  hl=2 l=   1 prim: INTEGER           :01
    7:d=1  hl=2 l=  71 cons: SEQUENCE
    9:d=2  hl=2 l=  10 prim: OBJECT            :1.2.156.10197.6.1.4.2.1
   21:d=2  hl=2 l=   7 prim: OBJECT            :1.2.156.10197.1.104
   30:d=2  hl=2 l=  48 prim: OCTET STRING      [HEX DUMP]:8[redacted]7
   80:d=1  hl=4 l= 722 cons: SEQUENCE
   84:d=2  hl=2 l=  10 prim: OBJECT            :1.2.156.10197.6.1.4.2.1
   96:d=2  hl=4 l= 706 prim: OCTET STRING      [HEX DUMP]:308[redacted]249

The OID 1.2.156.10197.1.104 means SM4 Block Cipher. The OID 1.2.156.10197.6.1.4.2.1 simply means data.

.sm2 files are an ASN.1 structure encoded in DER and base64-ed. The ASN.1 structure contains (int, seq1, seq2). Seq1 contains the SM4-encrypted SM2 private key x. Seq2 contains the x509 cert of the corresponding SM2 public key (ECC coordinates (x,y) of the point X). From the private key x, it is also possible to get X=x•P.

The x509 certificate is signed by CFCA, and the signature algorithm 1.2.156.10197.1.501 means SM2 Signing with SM3.

$ openssl x509 -inform der -text -noout -in publickey-test.cer
Certificate:
    Data:
        Version: 3 (0x2)
        Serial Number: 275466457874 (0x4023149312)
        Signature Algorithm: 1.2.156.10197.1.501
        Issuer: C = CN, O = China Financial Certification Authority, CN = CFCA ACS TEST SM2 OCA31
        Validity
            Not Before: Mar 25 08:39:36 2020 GMT
            Not After : Mar 25 08:39:36 2025 GMT
        Subject: C = CN, O = OCA31SM2, OU = [redacted], OU = Organizational-1, CN = [redacted]
        Subject Public Key Info:
            Public Key Algorithm: id-ecPublicKey
                Public-Key: (256 bit)
                pub:
                    04:[redacted]:7a
                ASN1 OID: SM2
        X509v3 extensions:
            Authority Information Access:
                OCSP - URI:http://ocsptest.cfca.com.cn:80/ocsp

            X509v3 Authority Key Identifier:
                keyid:04:C7:BC:F9:59:01:69:3E:8C:34:36:20:62:18:3C:DE:BC:B5:BB:0C

            X509v3 Basic Constraints: critical
                CA:FALSE
            X509v3 CRL Distribution Points:

                Full Name:
                  URI:http://210.74.42.3/OCA31/SM2/crl32.crl

            X509v3 Key Usage: critical
                Digital Signature, Non Repudiation
            X509v3 Subject Key Identifier:
                D3:08:18:06:3F:44:20:B4:33:9C:D0:86:90:50:52:FB:D2:69:8C:B3
            X509v3 Extended Key Usage:
                TLS Web Client Authentication, E-mail Protection
    Signature Algorithm: 1.2.156.10197.1.501
         30:45:02:21:00:91:21:53:91:02:07:34:17:70:bd:fb:6a:c8:
         51:8a:07:68:c5:12:54:0c:78:e1:d6:e4:6b:3e:8a:3b:14:fc:
         57:02:20:61:73:a0:e0:9e:db:90:68:fc:d2:43:c7:fc:0a:6c:
         43:1c:3d:2d:4e:57:65:f4:82:bd:52:03:c1:66:fc:04:d8

The equivalent Java code to read the private key x from a .sm2 file is:

import cfca.sadk.util.KeyUtil;
import cfca.sadk.algorithm.sm2.SM2PrivateKey;

[...]

SM2PrivateKey privKey = KeyUtil.getPrivateKeyFromSM2("file.sm2", "passphrase");
System.out.println(privKey.toString());

A utility to generate a random private key is also provided and can be used for production key generation. In there the SM2 elliptic curve parameters y² mod p = (x³ + ax + b) mod p can be found:

How to sign with SM2

Now that the private key x is known, it is possible to use it to sign the concatenation of parameters and return the PKCS7 format expected.

As a reminder, ECC Digital Signature Algorithm takes a random number k. This is why it is important to add a random generator to the signing function. This is also why it is difficult to troubleshoot: signing 2 times the same message will provide different outputs.

The signature will return 2 integers, r and s, as defined previously.

The format returned is PKCS7, which is structured with ASN.1. The asn1js tool is perfect to read and compare ASN.1 structures. For maximum privacy, it should be cloned and used locally.

The ASN.1 structure of the signature will follow:

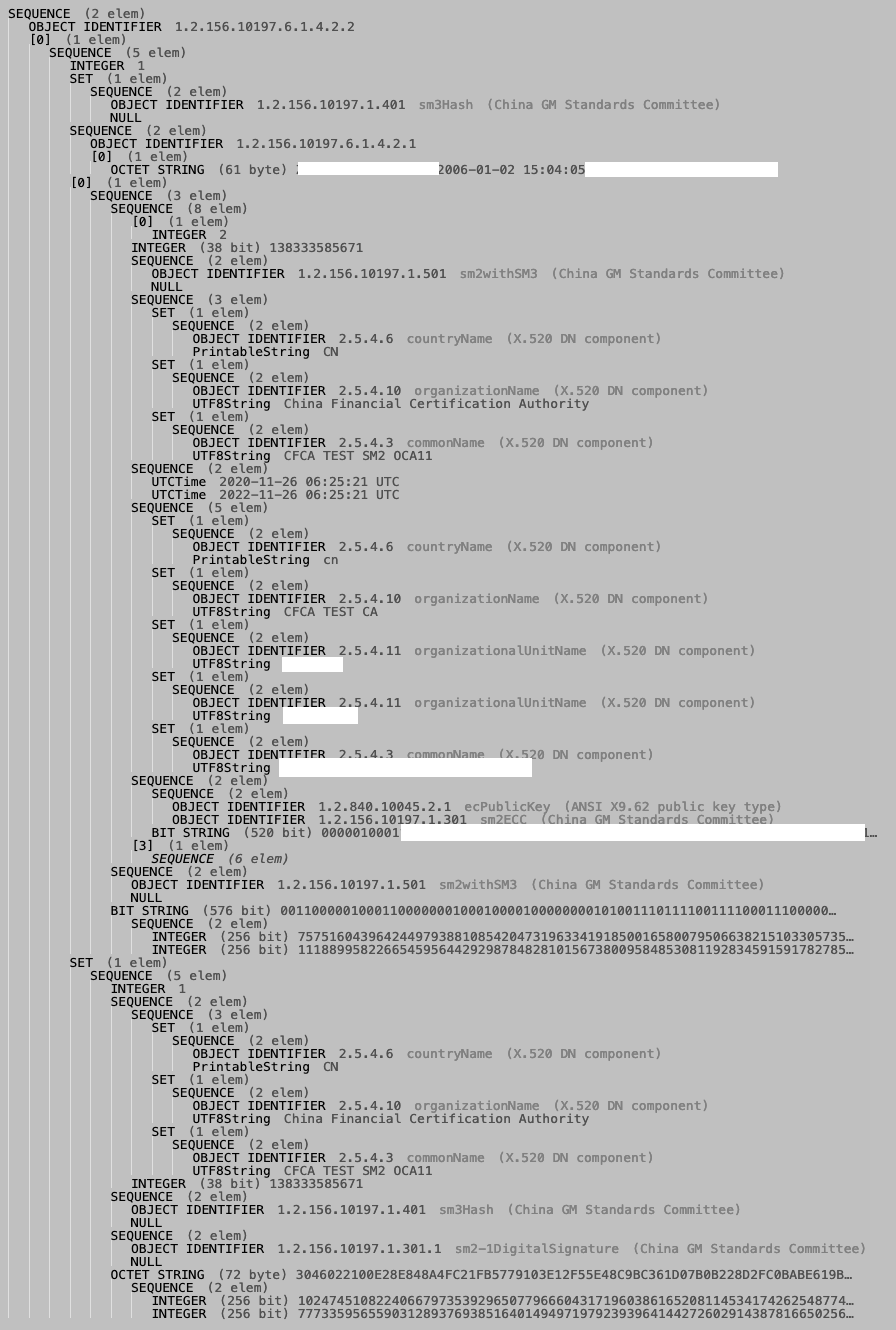signature
Screenshot from asn1js

To generate such signature, the Golang equivalent is:

import (
	"math/big"
	"encoding/hex"
	"encoding/base64"
	"crypto/rand"
	"github.com/tjfoc/gmsm/sm2"
	"github.com/pgaulon/gmsm/x509" // modified PKCS7
)

[...]

	PRIVATE, _ := hex.DecodeString("somehexhere")
	PUBLICX, _ := hex.DecodeString("6de24a97f67c0c8424d993f42854f9003bde6997ed8726335f8d300c34be8321")
	PUBLICY, _ := hex.DecodeString("b177aeb12930141f02aed9f97b70b5a7c82a63d294787a15a6944b591ae74469")

	priv := new(sm2.PrivateKey)
	priv.D = new(big.Int).SetBytes(PRIVATE)
	priv.PublicKey.X = new(big.Int).SetBytes(PUBLICX)
	priv.PublicKey.Y = new(big.Int).SetBytes(PUBLICY)
	priv.PublicKey.Curve = sm2.P256Sm2()

	cert := getCertFromSM2(sm2CertPath) // utility to provision a x509 object from the .sm2 file data
	sign, _ := priv.Sign(rand.Reader, []byte(toSign), nil)
	signedData, _ := x509.NewSignedData([]byte(toSign))
	signerInfoConf := x509.SignerInfoConfig{}
	signedData.AddSigner(cert, priv, signerInfoConf, sign)
	pkcs7SignedBytes, _ := signedData.Finish()
	return base64.StdEncoding.EncodeToString(pkcs7SignedBytes)

Modifications to tjfoc implementation

tjfoc PKCS7 utility was missing few things to fit the expected format. As such a fork has been created to accomodate it.

Disclaimer time. The resulting code is very specific and by no mean perfect nor reusable: it just works, and doesn’t do anything more than that.

How to reverse engineer Java functions

To debug Java, it is better to have a clean environment to start with:

Vagrant.configure("2") do |config|
  config.vm.box = "ubuntu/bionic64"
  config.vm.synced_folder ".", "/vagrant_data"
end

import java.nio.file.Files;
import java.nio.file.Paths;
import java.io.IOException;
import com.[redacted].sdk.service.impl.OpenApiSecurityService;

class HelloWorld {
    public static void main(String[] args) throws Exception {
        try {
            byte[] sm2Cert = Files.readAllBytes(Paths.get("certs-test/test.sm2"));
            OpenApiSecurityService securityService = new OpenApiSecurityService();
            String cfcaSign = securityService.cfcaSignature(signResource, "somepassowrd", sm2Cert);
        }
        catch(IOException e) {
            e.printStackTrace();
        }
    }

#!/bin/sh

javac -Xlint:deprecation -cp "JAR/*" HelloWorld.java
java -cp "JAR/*:." HelloWorld

Once the Java code is running in the VM, jdb is used:

vagrant@ubuntu-bionic:/vagrant_data$ jdb -classpath "JAR/*:." -sourcepath sources/ HelloWorld
Initializing jdb ...
> stop in com.[redacted].commons.cfca.SignVerUtils.signature
Deferring breakpoint com.[redacted].commons.cfca.SignVerUtils.signature.
It will be set after the class is loaded.
> run
run HelloWorld
Set uncaught java.lang.Throwable
Set deferred uncaught java.lang.Throwable
>
VM Started: Set deferred breakpoint com.[redacted].commons.cfca.SignVerUtils.signature

Breakpoint hit: "thread=main", com.[redacted].commons.cfca.SignVerUtils.signature(), line=28 bci=0
28    /* 28 */     X509Cert x509Cert = SM2CertUtils.getX509CertFromSm2(sm2CertData);

main[1] where
  [1] com.[redacted].commons.cfca.SignVerUtils.signature (SignVerUtils.java:28)
  [2] com.[redacted].sdk.service.impl.OpenApiSecurityService.cfcaSignature (OpenApiSecurityService.java:122)
  [3] HelloWorld.main (HelloWorld.java:52)
main[1] list
24    /*    */
25    /*    */
26    /*    */
27    /*    */   public static byte[] signature(byte[] sm2CertData, String sm2FilePass, byte[] sourceData, Session session) throws PKIException, UnsupportedEncodingException {
28 => /* 28 */     X509Cert x509Cert = SM2CertUtils.getX509CertFromSm2(sm2CertData);
29    /*    */
30    /* 30 */     PrivateKey privateKey = SM2CertUtils.getPrivateKeyFromSm2(sm2CertData, sm2FilePass);
31    /*    */
32    /* 32 */     Signature signKit = new Signature();
33    /* 33 */     String signAlg = "sm3WithSM2Encryption";
main[1] step
>
Step completed: "thread=main", com.[redacted].commons.cfca.SM2CertUtils.getX509CertFromSm2(), line=67 bci=0
67    /* 67 */     return CertUtil.getCertFromSM2(certBytes);

The commands where, list, step or next can be repeated until the code is understood. Keeping jd-gui open beside it to follow classes is also very helpful.

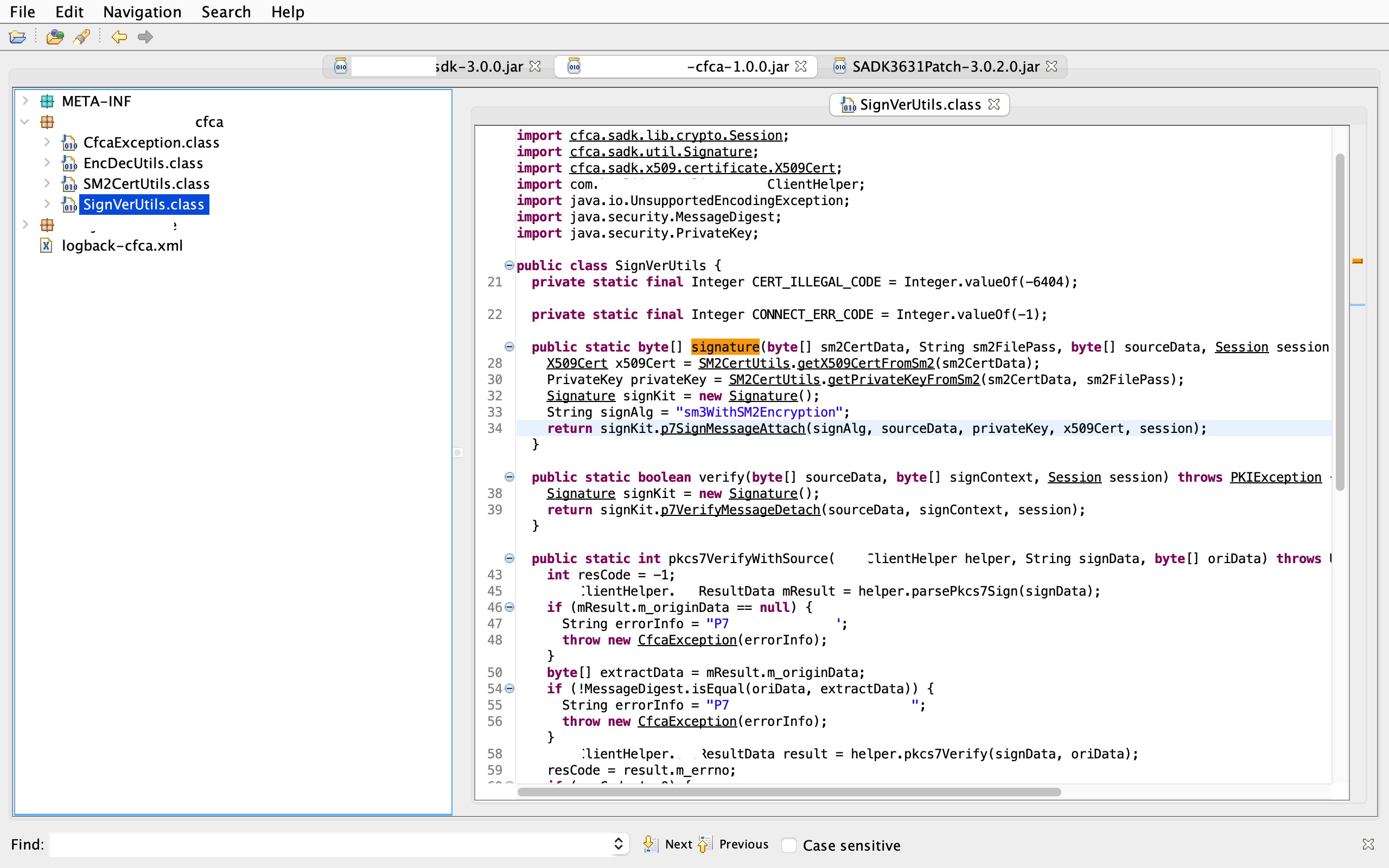jd-gui
Screenshot from jd-gui on the signature method

Key takeaways